医療統計学：用語集か行

▼▼▼▼▼▼▼▼ ▼▼▼▼▼▼▼▼
お問合せはこちらセミナー詳細こちら

医療統計学、医療経済学、数学のつぼをたとえ話でわかりやすく解説

運営者の20年以上にわたる医療統計学のノウハウを満載

回帰分析　反応変数を1つあるいは複数の説明変数の間の関係を仮定してその母数を推定することがあるが、その際の解析方法を指す一般的な用語。特別な例としては、ロジスティック回帰や多重線形回帰がある
回帰分析における変数選択法　回帰分析で反応変数を予測するのに、もっとも重要性が高い説明変数の組み合わせを選ぶための方法。以下の3つの方法がよく使われる。①前進選択法（変数増加法）：回帰式に説明変数がない状態から始め、これまでに選択した変数の組み合わせにある特定の変数を付け加えたときに予測能がどれくらいよくなるかを、何らかの基準によって評価することにより、変数をひとつひとつ付け加えていく。②後退除去法（変数減少法）：すべての説明変数を回帰式に含めた状態から始め、現在の回帰式からある変数をとったときに予測能にどのような影響があるかを評価することにより、説明変数を1個ずつ減らしていく。③段階的回帰（ステップワイズ法）：両者を組み合わせた方法。　この3種類の方法の中でいつでも一番ベストという方法はなく、適用に際してはいずれも十分な注意が必要である。
階級頻度　観測された変数について頻度分布を作ったとき、各階級に含まれる観測値の数
カイザーの規則　適当な数の成分を選ぶために主成分分析でしばしば用いられる規則。成分を観測値の相関行列から導いた場合、1より大きい分散をもつ変数のみを残すというのがこの規則の主旨である。
外挿　データ集合から、観測値の範囲外にある値を推定する手続き。たとえば回帰分析では、応答変数の値は、当てはめに使ったデータの範囲外にある新しい観測値に対しても、当てはめた数式に代入して推定することができる。
階層的モデル　ある観測値集合に対する一連のモデルで、各モデルはこのモデル群の中の別のモデルにパラメータを加えたり取り除いたりして得られる。交互作用項があり、交互作用に関係する説明変数のすべての低次の交互作用と主効果を含む交互作用項が存在するならば、階層的モデルは回帰分析や分散分析にも用いられる。
回想バイアス　特に後ろ向き研究で起こる可能性のあるバイアスの原因の一つで、一般的には対照群では被験者が曝露について報告をしないことが多く、実験群を対照群で申告に差があることから生じる。例えば、中絶と乳がんの関連を探す研究では、乳がんの患者は健康な女性と比べるとより正直に中絶について報告する可能性が高い。回想バイアスは、このような研究の結果を深刻にゆがめる危険がある。
外側観測値　第一4分位数から4分位範囲の1.5倍を引いた点と第三4分位数に4分位範囲の1.5倍を足した点で定義される領域の外側の値をもつ観測値。このような観測値は、外れ値の可能性があると見なされることが多い。
回答率　被験者の中で、郵便によるアンケートなどに対して、回答した人の割合
カイ2乗検定　この検定は、分割表を形成する2つのカテゴリー変数の独立性の検定にもっともよく使用されるが、他の目的、たとえば理論的な確率分布の観測データに対する当てはまりの具合の評価などにも用いられ、カイ2乗適合度検定と呼ばれる。この検定は観測された度数と期待度数との差の2乗に基づくものである。
カイ2乗分布　それぞれ独立に平均0、標準偏差1の正規分布に従うn個の変数の2乗和の分布。
介入指標　治療的あるいは予防的介入効果の推定値で、1人の早期の死を予防するためには介入によって何人の人のリスクレベルを変えるべきかを、危険にさらされた全人数に対する比率とした表したもの
回復期間　ウォッシュアウト期間
カオス　決定論的システムから生成された見かけ上ランダムな振る舞い。医学分野でこの概念がはじめて用いられたのは麻疹の流行い関するデータに対してであった。
確認バイアス　特に後ろ向き研究で、危険因子への曝露と関心事象の検出確率との関係から生ずるバイアスの一種。たとえば子宮頸がんの女性と健常対照群とを比較すると、経口避妊薬の服用例が患者群に多いという結果が得られる。これは服用群の方がより多くのスクリーニングを受けるためではないかと思われる。
確率　ある事象が起きる偶然性の定量的な表現。例えば、ある地域で生まれた10万人の子供の中で、5万1000人が男児であったとすると、男児が生まれる確率は0.51となる。
確率過程　確率的な規則によって経過が決まるような過程を表す確率変数の系列。医学における例としては、流行病や慢性疾患の患者数の推移がある
確率の加法則　2つの互いに排反な事象、すなわち同時には起こらない事象に対して、いずれかの事象が起こる確率は個々の確率の和となる。この法則は3つ以上の互いに排反な事象に対しても容易に拡張できる。
確率の乗法則　事象AとBが独立なとき、両方が同時に起こる確率はそれぞれの確率をかけたものである
確率プロット　観測した標本の分布の特徴を評価するための図で、データが正規分布をしているかを判断するのに使われることが多い。大きさの順に並び替えた標本値を、標準正規分布の分位数に対してプロットする。もし、プロットがほぼ直線なら、データは正規分布をしていると考えられる。
確率分布　離散確率変数の場合は、変数がそれぞれの値をとる確率を与える数式。例としては、2項分布とポアソン分布がある。連続確率変数の場合は、変数がある特定の区間の中の値をとる確率が、その下の面積によって表されるような曲線で、数式によって記述される。例としては、正規分布や指数分布がある。どちらの場合も、「確率密度」という用語も用いられる（密度と分布はときおり区別して扱われることがあり、そのとき分布は確率変数がある値以下をとる確率の意味で使われる）。
確率変数　どんな値をとるかが、ある特定の確率分布によって決まるような変数。例えば、正規確率変数は正規分布に従い、ポアソン確率変数はポアソン分布に従う。
確率密度サンプリング　症例―対照研究における対照群抽出方法の一つで、曝露におけるパターン変化に起因するバイアスを減少させることを目的とする。対照の抽出は、リスクにさらされている集団から、たとえば期間の終点といったような単なる時間の一点ではなく、症例が発生する全期間にわたって行う。
確率論的モデル　ランダムなまたは確率的要素を含むモデル
隠れた時間効果　観測値を収集するのに時間がかかったというだけの理由でデータに生じた効果
家系内再発生率　親族の1人が病気だったときに、ある人がその病気になる確率。遺伝相談で重要。例えば、トリソミー21はもっとも一般的な常染色体の異常で、その罹患率は出生数800に対して1であり、ダウン症を引き起こす。家系内再発生率は、病因によって異なり、2～15%である。
加重平均　各項目の相対的な重要性を適切に反映するために、各項目に重みを与えて求めた平均。たとえば、平均値が何個かあれば、各平均を導いた標本のサイズを重みとした重み付き平均を使ってひとまとめにできるだろう。
仮説検定　抽出したデータが母集団について述べられた内容と矛盾するか否かを判定する手続き一般をいう。
家族性疾患　遺伝的、文化的あるいは共通的環境などいろいろな理由から、家族的な発生傾向を示す疾患
家族性相関　遺伝子的に関連している個人間の表現型の形質の相関。相関の強さは形質の遺伝力と個体間の関連性の程度による
加速的死亡時間モデル　生存時間から成り立つデータのための一般モデルの一つで、ある個人について計測された説明変数が時間スケールに関して乗法的に作用し、したがって個人が時間軸上で進行する速度に影響すると仮定している。その結果このモデルは疾患の進行速度の見地から解釈ができる。
過大分散　1組のデータについて実際に計算した分散が、あるモデルを仮定した場合に予想される分散を超えている状況を表すのに使われる用語。離散データの解析でよくみられ、たとえば、2項分布を仮定した場合の割合や、ポアソン分布を仮定した場合の生起数などでこの現象がみられる。この現象は、観測値間の独立性の欠如の結果であることが多い。たとえば、反応変数が、多数の家族を観測して得られた、この1年間で病気になった家族の成員の割合だった場合、割合の値を算出するもとになる個々の2値の観測値は、独立ではなく相関があると考えられる。
片側打ち切りデータ　すべての患者が同時に試験に参加し、一定の時間後に試験が終了するような臨床試験で起こる打ち切りデータ
片側検定　たとえば、「ある母集団が他の母平均より大きい」のように、対立仮説に方向性がある場合に対する有意差検定。片側検定と両側検定の選択は、検定統計量を計算する前に行わなければならない。
偏りのある推定量　その期待値や平均値が母数の真値に等しくない母数の推定量。時々、偏りのない推定量でなく、このような推定量を使うことがある。それは偏りのある推定量が前者から得られる値よりも平均して推定すべき母数により近い値に導く可能性があるからである。これは、このような推定量の分散が偏りのない推定量の分散よりも十分に小さく、付随するバイアスを相殺する以上の効果があるためである。
勝ち馬に賭ける基準　治療結果が正（成功）か負（失敗）のどちらかであるような臨床試験でときおり使われる、データに依存した治療割り付けのルール。2種類の治療法のどちらかがランダムに選ばれ、最初の患者に適用される。次に、その治療が成功であれば同じ治療法が次の患者にも適用され、結果が失敗であればもう一つの治療法が適用される。このような試験計画を用いる目的は、成功率の高い治療群により多くの患者を割り当てながらも、治療の効果について信頼できる情報を将来の患者の利益のために集めることである。
活動的平均余命　与えられた年齢に対して、あと何年障害なしに過ごせるかの期待年数として定義される
ガットマン尺度　潜在変数（たとえば痛み）を測定すると称する2値変数の組に基づく尺度
カッパ係数　2人の判定者による判断あるいは診断の一致性について偶然による部分を調整した指標。それぞれ偶然の一致による分を引いた観測値の一致と可能な最大限の一致から偶然の一致分を引いた値との比として計算される。この係数は完全な一致のときに値1をとり、観測された一致が偶然による一致と等しい場合に0となる。偶然の一致とは、各診断カテゴリーについての各判定者の周辺和に従って計算された一致である。
仮定　統計手法が十分に根拠のある結果を与えるための条件。例えば、分散分析は通常、正規性、分散の一様性、および観測値の独立性を仮定している。
カテゴリカル変数　いくつかの属性の一つを観測値としてもつ変数。性別（男女）、血液型（A,B,AB,O）などが代表的な例である。これらの属性は、数字で表されることもあるが、数値としての意味をもつわけではない。
カテゴリーの併合　分割表にしばしば適用される方法で、2つ以上の行または列を1つにまとめて、各セルに含まれる観測値数を増やすこと。これにより間違った結論を導くことがあるため、通常は勧められない。
カリフォルニアスコア　乳児突然死症候群の研究で用いられるスコア。乳児に8個の有害な状態中何個がみられたかその数で示す。有害な状態としては、出生前の受診が11回未満、男児、3000g未満の出生時体重、25歳未満の母親などがある。
カルノフスキーの尺度　日常活動をうまく処理する能力の尺度。尺度は0（死）から10（正常、訴えなし、病気の証拠なし）までの11段階からなる。
ガルブレイスプロット　メタアナリシスにおける外れ値を同定するためのグラフを使った手法。基準化したエフェクトサイズを精度（標準誤差の逆数）に対してプロットする。もしも研究が同質であるならば、データ点は原点を通る回帰直線±2標準誤差の内部に分布するであろう。
カレンダープロット　臨床試験において各患者のコンプライアンスを記録する方法の一つで、1日あたりの薬の服用数をカレンダーに似た形で示したもの
環境疫学　生活の質や病気の発症などが、空気や水の汚染、危険物質の使用、食事や薬、職業、生活集権などの環境因子によってどのように影響されるかを研究する学問領域
間歇的ホルモンデータ　時間を追って血中ホルモン濃度の繰り返し測定を行う内分泌研究から得られたデータ。このようなデータは通常、視床下部における神経活動のバーストに反応して繰り返し現れるパルスの特徴的パターンを示す。
頑健な推定　理想的な条件のときだけでなく、仮定した分布またはモデルからかけ離れている場合でも、妥当な結果が得られる推定方法
監査証跡　データベースに生じた更新記録を保持するコンピュータープログラム
観察研究　研究者が調査中の事象に、ほとんどまたはまったく関与せず、危険因子とアウトカムの指標の関係が調査担当者の介入を受けることなく調べられる調査研究を指す用語。疫学の調査は疫学のほとんどの研究はこれに当る。このような研究の古典的な例としては、ドルとヒルが喫煙と肺がんの因果関係を明らかにしたものがある。
間接基準化　既知の基準集団を使用して生の死亡率やいくつかの変数に関する罹病率を調整すること。そのためには、たとえばがんの死亡率を独身女性と既婚女性の間で比較するような場合には、これら2群の間に当然あるはずの年齢分布差を調整しなければならない。基準集団の年齢別死亡率を各群の年齢分布に適用し、各々における死亡数の期待値を得ればよい。この値から各群の相対的な死亡率が得られる。
感染確率　おもにAIDSの伝播の調査で使われる用語で、HIVに感染したパートナーから1回の性交で感染する確率を指す。
感染間隔　1人目の患者の症状が観察された時間から、その患者から直接に感染した2人目の患者の症状が認められた時間までの間隔
感染期間　感染の進行を記述する用語で、潜伏期間の後に来る期間をいう。この期間には、感染した患者は何らかの形で感染物質を放出し、他の人に病気をうつす可能性がある。
完全事例解析　いずれの変数にも欠測値のないデータだけを用いて行う解析。この方法は有効標本サイズが小さくなり、解析結果にバイアスを生ずることも多い。
感染速度　感染症の起因物質が、環境を伝わる速さ、または他の人へ感染する速さ
感染の連鎖　ある個体集団の間に感染が生じていく経路を記述する方法の一つ。最初の患者との直接接触で感染した個体を第1世代と呼ぶ。第一世代との直接接触で感染した個体を第2世代と呼び、以下同様に名付ける。各世代の患者数を順番に並べたものを感染連鎖という。1-2-1-0という系列は、初期患者数が1、第1世代患者数が2、第2世代患者数が1、第3世代以降の患者数が0を意味する。具体的な例としては、ある地域の男性と別の地域の女性との間の、防具を用いない性交によるHIVの伝達などがある。
完全連結クラスター法　凝集型階層的クラスター法の一つで、2つのクラスター間の距離を2つのクラスターに属する成員間の最大距離として定義したもの
感度　診断テストの性能の指標で、病気をもっている人が正しく病気だと分類される割合、つまり、病気の場合に、検査結果が陽性となる条件付き確率。病気の患者の大部分に対して陽性となる検査は、「感度」が高い。検査の第一の目的が病気の発見である場合は、感度が高いことが重要である。
感度分析　仮定のどれかを変えると最終的な解釈や結論が変わるかどうかを評価するための、一連のデータ解析
管理用データベース　健診システムの運営のための日常的かつ系統的に集められた情報から得られたデータベース。このデータは入院手続きや在院期間を調べ、病院間、地域社会間での比較のために使われる。
関連性　2つの変数間の関係を表す一般的用語。基本的には相関と同じ意味である。2×2分割表を構成する2値変数の関係について使われることが多い。
関連性の指標　2つ以上の定性的な変数間の、統計的な関連度の強さを定量化する数値的な指標。
疑陰性率　病気を有する被験者の中で診断テストによって病気でないと診断された症例の割合
幾何分布　ベルヌーイ行列で最初の成功が得られるまでの失敗の回数Nの確率分布
幾何平均　歪んだデータに対して適した位置の指標。n個の観測値の積のn乗根で与えられる。
期間バイアスを伴う標本抽出　外来で標本抽出を行う場合に起こるバイアスで、来院する頻度が高いというそれだけの理由で、その患者が標本に選ばれる可能性が高くなることが原因となる。例えば、がんのスクリーニング調査で見つかった症例の標本では、症状が出て陽性と診断された症例の標本より進行の遅いがんの症例が多い傾向がある。
棄却域　帰無仮説を棄却する検定統計量の値の範囲。棄却域の大きさは、帰無仮説が真のとき、結果がこの領域に属する確率、すなわち第1種の過誤の確率となる。
棄却限界値　標本データから計算したある統計量がこの値より大きい場合、帰無仮説を棄却することとなる限界値。この値は選択した有意水準によって決まる。
危険因子　個人の行動や生活の様式、環境中の有害物質への曝露、または生まれつきや遺伝的な特性で、特定の病気や健康状態と関連があると考えられるもの。
疑似実験　実験に似ているがある特性には弱点がある研究。特に被験者の割り付けを調査者がコントロールできない研究に対して使われる用語。たとえば、自然災害が健康に及ぼす影響に関心があるとき、自然災害の被害者とそうでない人を比較することはできるが、被験者を意図的に（ランダムであろうとなかろうと）2つのグループに割り当てることはできない。
疑似独立性　分割表における独立性の形式の一つで、表の特定の部分に限定した場合に成り立つもの。
疑似尤度　観測値に対して特定の分布を仮定することが不可能、または好ましくなく、そのため尤度を記述できないときに、母数推定の基礎として使われる関数。関数は、観測値の平均と分散との間に仮定した関係によって決まる。一般化線形モデルを適用するとき、過大分散が生じる場合に使われる。
記述統計学　データを要約し、表にまとめる統計手法。平均値と分散を計算し、ヒストグラムをプロットするなど、データの主要な特徴をわかりやすく示す方法。
基準集団　調査対象の母集団と比較をする標準の母集団
寄生虫数検査　糞便を定量的に滴定した標本中の虫体やその嚢胞または卵の計測数に基づく腸内寄生虫感染の監視法
季節変動　厳密には時系列における年周期の現象を指すが、単に周期的な動きを指す言葉としてもよく使われる。感染症の季節的な変動は、例外的というよりむしろ規則的なものであり、大気の状態の変動、病原体の流行具合や菌力、宿主の行動などに影響される。
既存対象（ヒストリカルコントロール）　過去に標準的治療法で処置を受けた患者群を、現在の患者に対する新しい治療法の評価を行う場合の対照群として用いる場合をいう。この方法は医学研究ではかなりよく使われるが、時間の経過によって変化する他の要因に起因するバイアスを十分に取り除けないため、勧められない。
期待値　ある特定の確率分布をもつ確率変数の理論的平均値
期待度数　分割表の解析で使われる用語で、興味のある仮説のもとで期待される値の推定値をいう。たとえば2次元の表の場合、2つの変数が独立であるという仮説のもとでは、あるセルの期待度数はそのセルが属する行の合計と列の合計の積を観測値の総数で割ったものとなる。
基本感染数　感染症の理論で用いられる用語で、完全に感染可能な集団において1症例が引き起こすであろう2次的な症例の数を表す。この数は、感染期間の長さ、1回の接触の間に感受性がある個体に感染する確率、および単位時間あたりに接触した感受性がある新しい個体の数に依存するので、異なった感染症で、また同じ感染症でも異なった集団でかなり変化すると考えられる。基本感染数の値が大きければ大きいほど、流行を防ぐために免疫を受けなければならない人口の割合が大きくなる。
帰無仮説　「差がない」または「関連がない」という仮説で、「差がある」または「関係がある」という対立仮説に対して（通常は有意差検定により）検定を行う。
逆計算　感染から発症までの潜伏期間についての知識を用いて、観測された疾患の発病率から逆に計算することにより、ある伝染病の過去の感染率を推定する方法。主としてAIDSの発生数データから妥当と思われるHIV発生数曲線を再構成するために使われる。この方法の限界としては、最近の感染率についての情報をほとんど与えないことと、最近の発生数の予測値が不安定となることである。
逆数変換　1/確率変数、の形の変換。ある種の変数には特に有用で、たとえば、抵抗はこの変換でコンダクタンスになり、時間は速さになる。ときには、この変換により変数間に線形の関係が成り立つことがあり、たとえば、肺の容量変化と気道抵抗の関係は非線形だが、肺容量変化に対する気道コンダクタンスの関係は線形になる。
逆正規分布　1つの粒子が血中にとどまる時間の長さ、妊娠データ、入院期間などの現象を記述するのに使われてきた確率分布。
逆正弦変換　比率を表す確率変数の変換の一つで、分散を安定化した分散分析や回帰分析などの解析手法に適した値とするために用いられる。
急進統計団体　英国の社会科学者の全国的なネットワークで、政策決定過程で用いられる統計に対して批判を行う。この団体は、例えば保健とか教育の分野で批判力のある市民の能力を育てることも目的としている。
級内相関　測定用質問表の「真の」値についての対象間ばらつきに起因する観測値の分散の割合。この相関は、多数の判定者が多数の対象について、興味ある変数の点数を付ける試験から推定することができる。
競合リスク　多くの危険因子にさらされる個人の集団における死亡率パターンの研究で使用される用語。例えば、肺がんの危険因子としての喫煙を研究する場合、冠動脈性心疾患は競合するリスクとなる。個々の危険因子の影響をいかに分離しうるかが問題となる。
凝集型階層的クラスター法　クラスター分析の方法の一つ。最初は各個体を別々のクラスターと見なし、次々とそれらを結合する操作を続け、最後は1つのクラスターになるまで行う。各ステップでは、適当な距離の定義に従って、互いにもっと近い距離にある個体もしくは個体群を結合する。この全ステップは樹形図によって表される。特定のクラスター数に対応する解は、樹形図をあるレベルで切ることによって得られる。
疑陽性率　病気でない被験者の中で、診断テストによって病気であると診断された症例の割合
共存症　1人の患者や同一の家族などに2種の障害が共存すること。疾患は内科的なものでも精神科的なものでも、あるいはアルコール依存症を含む薬物使用によるものであってもよい。共存する疾患は同時あるいは連続的に起こる。しかし、2種の疾患が共存するということは必ずしも一方の疾患が他方の原因であることを意味しない。
共通単位変数　同じスケールもしくは同じ単位で測られる変数。例えば、収縮期血圧と拡張期血圧など。
共通媒体による伝播　ある病気にかかった人に共通な原因からの病原物質の伝播。共通の媒体には、空気、水、食品などがある。
共同研究　多施設共同試験と同じ意味で使われる用語
共分散　2変数に対する関連性の指標で、各変数それぞれの平均値からの偏差の積の平均で表される。
共分散分析　基本的には多重線形回帰の一種で、説明変数のいくつかがしばしば2値のカテゴリー変数（例えば治療群）でその他が連続変数（例えば年齢）であるものをいう。この解析の目的は、治療間の差の評価に使うF検定の感度を上げることにある。
共変量　回帰分析においては説明変数と同じ意味で使われるが、もともとは、主要な関心の対象ではないが解析を行うに当たっては考慮すべき変数といった意味をもっている。
寄与危険度　特定の因子への曝露と、あるアウトカムのリスクとの関連性を表す量である。特定の1因子に起因する罹患率の大きさを評価する量であり、症例―対照研究および横断的研究から推定することができる。例えば終身喫煙者の場合、全肺がん症例の31%が喫煙以外の5つの危険因子によることが報告されている。
局所オッズ比　大きな分割表中の隣り合った行と列からできる2×2分割表のオッズ比
局所重み付き回帰　回帰分析で説明変数のある場所の近傍における回帰式を近似するのに、1次または2次の多項式を使う方法。何らかの構造がもっとはっきりわかるように散布図を平滑化したり、説明変数と反応変数の間の非線形の関係を求めるのに有用。とびはなれた値の影響で平滑化が歪められてしまうのを避けるために、ロウエスとして知られている頑健な推定方法が使われる。この計算過程は、本質的には逐次重み付き最小2乗法である。
曲線下面積　縦断研究や用量―反応関係などで得られるある個体で時間経過を追った観測値を要約するためによく使われる方法。通常、相続く2つの時点間の曲線下面積を加えあわせて計算する。曲線下面積は毒性や薬物の効果といった生物学的影響の予測値としてよく使われる。一定の時間間隔で集められた測定値の場合、AUCは本質的に平均値を使用することと等価である。
許容可能リスク　特定の医学的処置の利益が潜在的な危険に勝ると考えられる場合のリスク。例えば膵島移植はⅠ型糖尿病の多数の2次的効果をコントロールするのに役立つだろうが、レトロウィルス感染の危険性を考えると、移植を行う場合のリスクレベルをどの程度と考えればよいだろうか。
許容区間　平均的にまたはある信頼度で、少なくとも母集団の一定の割合を含む区間。将来の値についてのことが多いが、確率変数の値の不確定度を要約するのに使われる。
許容限界値　ある作業環境の空気の中に（ガスとか蒸気とか粒子にして）存在する化学合成物質の最大許容濃度で、現在の知識では通常は労働者の健康を損ねたり過度の不快の原因とはならないとされる値。
均衡状態　臨床医が次の患者をある方法で治療するか、別の方法で治療するかの選択に関して完全にバランスがとれた状態。均衡状態はすべての臨床試験の前提条件であり、臨床試験の目的は、医療に対して影響を与えるために試験完了時までに意図的にこの均衡を覆すことである。
近似　正確ではないが、実用上役に立つ程度に十分に正しい結果をいう。
空間データ　いくつかの場所でとらえた変数の測定値または計測結果の集まりで、この場合、データの空間的な構造に関心がある。例えば、ある国の異なる地域における呼吸器系のがんによる死亡者数
偶然ゼロ頻度　標本の大きさが不適切だったために、分割表のセルの頻度がゼロとなること。
偶然の一致　見かけ上何の因果関係もないと思われる事象が、意味のありそうな関係として同時に起こること。このようなことは日常的にもよくあり、驚きのもととなる。しかしながら、フィッシャーが指摘しているように、「100万に1つのできごとでも、それはその正しい頻度で実際起きるのである。それが自分の身に起こったとしたら、どんなに驚くことであろうか」
クォーターサンプル　各標本単位は完全にランダムには抽出されないが、例えば、40歳以上の男性10名とか、35～45歳の女性25名というように、各カテゴリーの中である個数の標本単位がランダムに抽出されるような標本。世論調査でよく用いられる。
クォリティーオブライフ　人が、身体的、精神的、社会的にどの程度活動できるかについての自分自身の認識
区間打ち切り観測値　ある特定の事象が起きるまでの経過時間に関する研究で、被験者が連続的に観察されていない場合にみられる観測データをいう。言い換えれば、ある事象が生じた時刻は、特定の観察時点（例えば検査日）より前であったということしかわからない。
具象化　潜在変数に名前を付けて、QOLとか人種的偏見のような事柄を、たとえば長さとか重さのような物理的な量であるかのように議論を行うこと。
薬の有害反応に対する米国国立がん研究所の基準　薬の有害反応を評価するための尺度。なし、軽度、中程度、重症、命に関わる、死亡　の6段階からなる。連続変数（例えば白血球数）もカテゴリー変数（例えば吐き気）も両方ともこの順序尺度に変換できる。
クーダーリチャードソンの公式　項目が、例えば賛成・反対やはい・いいえのように、2種類の答えしかもたないテストの内的整合性または信頼性の尺度
グッドマン‐クラスカルの関連性指標　分割表を構成する2つの変数間の関連性の強さを測るための一連の指標。各指標はそれぞれ特定の問題を対象として作られている。特に、順序変数と非順序変数では異なる指標が用いられる。また、1つの変数が説明変数と見なされ、他の変数が応答変数と考えられる場合も同様である。
組み換え頻度　組み換え体の数を子孫の総数で割ったもの。この度数は、遺伝子地図上の座位間の相対的な距離を評価する手助けとして使われている。
クラスカル‐ワリス検定　一元配置分散分析に類似の、分布によらない方法で、複数の母集団が互いに同一の中央値をもつかどうかを検定する。
クラスター‐サンプリング　母集団の構成要素を複数のグループ（クラスター）に分けて行うサンプリングの方法。多くのクラスターを無作為に選びだした後、そこから標本を抽出する。クラスターとしては、家族、病院、学校など、自然なグループ分けを使うことが普通である。
クラスター分析　各個体について観察した変数値を用いて、最初は分類されていないデータの集まりから、（望むらくは）理解可能で情報を提供する分類結果を構成するための一連の方法。
クラスター無作為化　個人のグループあるいはクラスターを無作為に割り付けること。処理グループを作る場合に、個人ではなく、例えば、家族、病棟、学校のクラスに割り付ける方法。個人レベルでの無作為割り付けに比べて統計的に効率が良いわけではないが、経済的である、実行が容易、倫理的に好ましいなどの利点があることが多い。
クラスタリング　もっとも普通には、空間的、時間的、あるいはその両方における事象の規則的でないグループ分けに対して使われる。このグループ分けを行うためには、疑われる原因物質の同定を行うための調査を必要とするかもしれない。
クラス幅　1組の観測値をいくつかの階級に分けて頻度分布を構成したときの、各階級の幅。
繰り返し測定の分散分析　縦断的データを解析するための分散分析。この解析の基礎は簡単な混合効果モデルである。この方法は、繰り返し測定の分散共分散分析行列が球状性を満たし、かつどの治療グループの分散共分散行列も等しい場合のみ適用可能である。
グリーンウッドの公式　生存関数の積極限推定量の分散を与える公式。
グリーンハウスガイザーの補正　繰り返し測定値の分散共分散行列が複合対称の仮定から逸脱する場合に、繰り返し測定の分散分析で使われるF検定の自由度を調整する方法。
グループ化された２値データ　たとえば同じ診断を受けていたり、性質が同じであるような患者または対象者に対して、２つの可能な属性のうち一方の割合を使って集計されている２値データの観測値。
グループ分けデータ　区間内の観測値の度数を記録したデータ。
クレメセンのかぎの手　年齢ー期間ーコホート分析により母数の推定値を解釈する際に、時として観察される現象。死亡率がある最大値まで増加し、それから引き続き上昇傾向が続く前にいくらか低下することを指す。
クロスオーバー計画　個々の治療の差を調べることを目的として、患者に一連の治療法を順次割付ける臨床試験の方法。各治療法を割り付ける順序は無作為に与える。もっとも簡単な計画は２つの治療AとBによる２群の計画である。一方の群はA,Bの順序で、他方の群はB,Aの順序で治療を行う。これを２X2クロスオーバーデザインと呼ぶ。治療法の比較は患者間というよりは患者内で行うものであるので、必要な統計的検出力を得るための例数は比較的少なくてよい。このような計画の解析は、繰り返し効果、すなわちある患者のある期間におけるデータを解析するとき、その結果が現在の治療のみならずその前に行った治療の影響を受けるという効果のために複雑となり、２つの治療効果を分離することが難しい。そのため、２つの治療の間にウォッシュアウト期間をおくなどの措置を講ずるが、そもそもこのような方法は繰り返し効果が排除できる場合にのみ使えると主張する研究者もいる。クロスオーバー計画が適用できるのは、完全な治療ではなく短期間の症状の緩和が目的とされるような慢性の状態に限られる。クロスオーバー計画の利点はその効率と治療に対する患者個人の反応を検討できる点にある。
クロスオーバー比　臨床試験において、最初の無作為割付から別の治療法へ変更された患者の割合
クロンバックのアルファ　「はい」と「いいえ」の回答からなる心理学テストにおいて、内的整合性を測る指標
警戒線　管理図で、望ましい水準からの乖離の程度が軽い範囲を示す線。
経験的　基本法則や理論からの演繹ではなく、観察と経験に基づくこと。
傾向スコア　臨床試験にある層の人がどれくらい参加しているかを記述するパラメータで、一連の随伴変数の値が与えられたときに、ある治療が割り付けられる条件付き確率として与えられる。結果の解釈の際に、ランダムでない治療割り付けやランダムでない選択を調整するのによく使われる。
計数データ　ある尺度により測定するのではなく、何らかの興味ある事象が生じた回数を数えて得られたデータ。各個人の虫歯の数などがよい例であり、ポアソン分布やポアソン回帰を使って解析することが多い。
計数反応法　各群の被験者に、異なる用量の、通常はそれぞれ被験者の一定割合が反応する。薬を投与する実験、このような分析データは、しばしば「プロビット変換」を用いて解析され、中央値有効量や50%致死量の推定が主な関心の対象であることが多い。
系統誤差　データ収集や解析の方法に問題があり、本来推定したい量から結果が偏ってしまう場合に生じるバイアス。偶然誤差と異なり系統誤差は標本数を増やすことによって解決することはできず、単にバイアスのある推定量をもっと「正確に」求めることになるだけである。
系統的レビュー　ある特定の問題に関して、一定の基準に合致しているすべての研究に対する論評。特に、臨床試験の結果の調査で重要。このような論評のもっとも重要な側面は、どのようにして対象の研究を選択したかと、どのようにして関連のある（そして満足できる）研究をすべて取り上げたことを保証するかである。選択したすべての研究が利用可能になれば、次の過程では一般にそれぞれの研究から得られたエフェクトサイズのメタアナリシスを行うことになる。
系統的割り付け　臨床試験で患者を割り付ける方法で、たとえば、誕生日の日付が偶数の人には治療Aを行い、奇数の人には治療Bを行うような、何らかの系統的な方法でランダム割り付けを模倣することを目指したものです。原則としてバイアスはありませんが、割り付け方法が公開されていることとそのため現場で正しく割り付けが行われない可能性があるため、問題が起こることである。
軽便手法　かつて分布によらない方法に対して使われた用語で、おそらく計算が簡便なことと、対応するパラメトリックな手法より劣ると考えられたことからきているのだろう。
形容詞的な尺度　形容詞的な記述の尺度。連続的な回答と不連続的な回答がある。それぞれの例として以下の２つがある。①不連続的回答（参加者は１つを丸で囲む）：今日はどの程度の痛みを感じましたか？（平均以下、平均、平均以上）　　　②連続的回答（参加者は直線のどこかに印を付けてください）：あなたは治療にどの程度満足していますか？（きわめて不満足、不満足、どちらでもない、満足、大変に満足）
計量生物学　生物現象の観察に基づく数値データの研究に対して統計手法を適用すること。
系列相関　縦断研究で、同一被験者に対する測定値の間でよくみられる相関。この相関の大きさは、測定の時間間隔に依存することが多い。間隔が大きくなれば、ふつう相関は減少する。正しい推論を行うためには、縦断調査データの解析では系列相関を適切にモデル化する必要がある。
ケースミックス　個々の臨床医、病院、あるいは診療所で取り扱われた患者あるいは医学的問題の諸特性
ケチの原理　あるデータに適切に当てはまるモデルの中では、パラメータ数がもっとも少ないモデルが好ましいという一般的な原則。
月間妊娠率　１ヶ月間に妊娠をする確率。妊娠を望んでいる受胎能力のあるカップルでは約20%ある。説明できない不妊がみられるカップルについての臨床研究では、この率は2～5%に激減する。このようなカップルに対する治療（たとえば、試験管受精）の適切性は、この数字から妊娠の割合をどれだけ上げうるかによって判断すべきである。
血清学的データ　個体の抗体の有無が血清学的な検査を使って調査されることによって得られるデータ。たとえば、異なる年齢群間で血清抗体陽性の個体の割合が記録される。
欠測値　何らかの理由によりデータから欠落した観測値。縦断研究では欠測値は特に問題である。欠落が起こる理由はさまざまであるが、たとえば、被験者が研究から完全に脱落したとか、予定の訪問時に来なかったとか、測定装置の不良などがある。患者が早期に参加をとりやめる一般的な原因としては、病気が治癒したこと、逆に改善がみられないこと、研究中の治療によると思われる望ましくない症候が起きたこと、逆に改善がみられないこと、研究中の治療によると思われる望ましくない症候が起きたこと、調査手順が不愉快なこと、別の健康上の問題が併発したことなどがある。欠測値は解析方法を非常に複雑にすることが多いが、データが完全に揃った被験者だけを取り扱うだけではたいていは不十分である。欠測値のあるデータを解析するには、完全にランダムな欠測（MCAR）なのか、ランダムな欠測（MAR）なのか、情報のある欠測なのかにより、異なるアプローチが必要になる。MCARは被験者が、観察された測定値と、もし欠損していなかったときに得られるであろう測定値の両者に対して独立な過程で研究から脱落するときに発生する。このとき、すでに得られた観測値は事実上、すべての被験者の観測値の単純な無作為標本となります。
MARは、脱落の確率がそれまでの反応値に依存するが、脱落後の将来の（記録されない）値には条件付き独立の場合に起こる。最後に情報のある欠測の場合、脱落の機序は結果変数の未観測の値に依存する。
決定木　意志決定問題における選択肢を図で表したもので、意志決定者により予想されるすべての可能性を網羅している。たとえば、次のような問題を考える。医師がある患者について２つの治療を選択しなければならないとする。患者は２つの疾患のうち一つであることがわかっているが診断は確定していません。患者の精密検査によっても診断は確定せず、患者が疾患Aである確率はpであることしかわからない。この問題の決定木は図のように表される。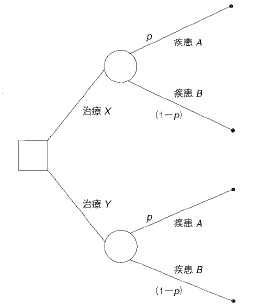

決定計数　意決定係数