医療統計学における推定と検定

標準誤差を実際に計算するときは、先の10人の年齢データの例では標準偏差を標本の大きさの平方根、ここでは√10で割ります。標本が大きいほど、細いつりがねになります。

100個の標本平均は中心極限定理により正規分布をしていますから、この100個中68個の標本平均は、平均値±標準誤差の範囲に入るということになります。標準偏差はデータのばらつきですが、標準誤差はそうではなく、標本平均のばらつきです。標本平均は母平均の推定値ですから、標準誤差が小さいということは、母平均の推定精度が高いということになります。

95%信頼区間は、100個中（68個ではなく）95個入るような範囲です。つまり、平均値±標準誤差の範囲より広くなります。具体的には、標準誤差をt倍します。

つまり平均値±t×標準誤差　が計算式です。標準誤差と同様、この範囲が狭いほど、母平均の推定精度が高いということです。tは2に近い値です。

＜ｔ検定＞

Ａ群　　28歳　30歳　33歳　38歳　40歳　43歳　46歳　49歳　51歳　52歳
Ｂ群　　20歳　22歳　25歳　30歳　32歳　35歳　38歳　41歳　43歳　44歳

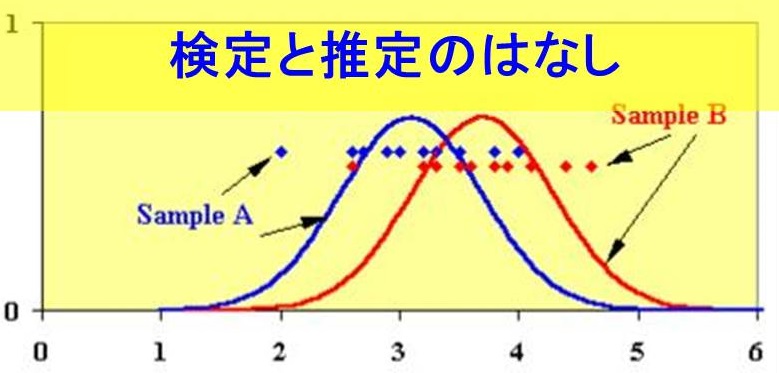
10人のＡ群と、別の10人のＢ群（独立2群）で、年齢の差があるかどうかを考えます。

その際に、先ずＡ群とＢ群は年齢に差がないと仮定します。

この仮定が成り立つｔ分布の確率が5%を切る場合、上の仮定は20回に1回すら起こり得ない稀なことであると判断し、上の仮定を棄却しＡ群とＢ群は差があるとします。

これが独立2群のt検定です。実際に検定をすると、5.4%となり5%を切らないので、仮定は棄却されず、Ａ群とＢ群は差があるとはいえない、という結論になります（差がない、という結論でないことに注意）。

ところで、Ｂ群はＡ群の8年前のデータだとした場合はどうでしょう。

この場合は独立2群ではなく、同じ群を8年前と比較するわけですから対応のある2群ということになり、この場合は対応のあるt検定を行います。独立2群に比べると有意差は出やすくなります。

実際この場合、2.7%で5%を切り仮定は棄却され有意となります（Ａ群とＢ群は差があるという結論です）。