多角形の外角の和
多角形の外角の和
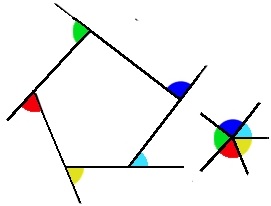
図形には内角と外角があります。
図形の内側にある角が内角で、1つの角と隣り合う1辺を延長した外側にできるのが外角です。
角が増えれば、当然のことながら内角の合計は大きくなります。
三角形なら180度、四角形なら360度といった具合です。
となると、外角の合計も増えるのではないかと思えますがそうではありません。どんな多角形であっても、外角の合計は必ず360度になります。
これは多角形の内角の和を求める公式で証明することができます。
1つの角における内角と外角の合計は180度になるので、n角形のすべての内角と外角の和は180度×nとなります。
この計算から内角の和「180度×(n−2)」を引いた、180×n−180×(n−2)=360(度)が外角の和となります。
実際に数字を当てはめてみるとよくわかります。
たとえば、三角形ならば「540−180」(度)、七角形なら「1260−900」(度)でいずれも360度となります。
⇒ 地図の縮尺
医療統計学:多角形の外角の和 関連ページ
- 医療統計学:暗算のコツ
- 医療統計学:地図から距離を知る
- 医療統計学:不快指数
- 医療統計学:5kgの減量
- 医療統計学:魚の数の数え方
- 医療統計学:ブロック式計算術
- 医療統計学:回転寿司の勘定
- 医療統計学:利子の暗算
- 医療統計学:土地の査定
- 医療統計学:同じ誕生日
- 医療統計学:誕生日を当てる
- 医療統計学:記念日の曜日
- 医療統計学:濃度の計算
- 医療統計学:高速道路
- 医療統計学:元号を西暦に直す
- 医療統計学:繰上げと繰下げ
- 医療統計学:概数をおさえる
- 医療統計学:割引価格の計算
- 医療統計学:3桁区切りの意味
- 医療統計学:魔法の計算術
- 医療統計学:千代田区の人口
- 医療統計学:平均年齢
- 医療統計学:摂氏と華氏
- 医療統計学:無量大数
- 医療統計学:素数について
- 医療統計学:四捨五入
- 医療統計学:内外価格差
- 医療統計学:エラトステネスの篩
- 医療統計学:倍数の見つけ方
- 医療統計学:デカルト座標
- 医療統計学:地図の縮尺
- 医療統計学:多角形の対角線の数
- 医療統計学:円グラフと棒グラフ
- 医療統計学:割合の計算
- 医療統計学:田の字の計算術
- 医療統計学:以上以下未満
- 医療統計学:メートル法
- 医療統計学:クラウド
